연금 포트폴리오 종목 선정하기 (feat. 유전알고리즘)
portfolio optimization
안정적인 노후를 위해 연금투자를 하고 있습니다. 장기적으로 지켜봐야하는 연금저축을 어떻게 하면 잘 할 수 있을지 고민이 됩니다.
투자를 위해서는 1)투자 종목 선정과 2)투자 비중 3)리밸런싱 주기를 잘 선택해야 합니다.
적극적인 행동으로 수익률 최대화, 수수료 최소화를 위해 리밸런싱 주기는 1달로 두었습니다.
리밸런싱 일자는 매월 첫 영업일로 두었고, 월 실적은 말일기준으로 하였습니다.
투자비중 선택은 샤프비율 최대화라는 로직으로 고정하였습니다.
결국 종목선정을 잘하는 것이 이 글의 목적입니다.
좋은 종목 선정하는 것은 매우 어려운 일인 것 같습니다.
- 투자비중 선정 : MSR(Maximize Sharpe Ratio)
- 종목선정 방식 : 몬테카를로, 유전알고리즘
- 리밸런싱 주기 : 매달
- 하이퍼파라미터
- 종목개수 (5종목)
- 투자비중 선정방식(MSR)
- 롤링 윈도우 (12개월)
- 그외 유전알고리즘 파라미터들
라이브러리
from pykrx import stock
import requests
import json
from pandas.io.json import json_normalize
import pandas as pd
import datetime
import time
from tqdm import tqdm
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
from scipy.optimize import minimize
import quantstats as qs
#matplotlib 한글 폰트 출력코드
import matplotlib
from matplotlib import font_manager, rc
import platform
try :
if platform.system() == 'Windows':
# 윈도우인 경우
font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf").get_name()
rc('font', family=font_name)
else:
# Mac 인 경우
rc('font', family='AppleGothic')
except :
pass
matplotlib.rcParams['axes.unicode_minus'] = False
1. Crawling
ETF 종목명 불러오기
# https://yobro.tistory.com/197
date = datetime.datetime.now().strftime("%Y%m%d")
tickers = stock.get_etf_ticker_list(date)
tickers=pd.DataFrame(tickers,columns=['종목코드'])
url = 'https://finance.naver.com/api/sise/etfItemList.nhn'
json_data = json.loads(requests.get(url).text)
df = json_normalize(json_data['result']['etfItemList'])
df=df[['itemcode','itemname']]
df=df.rename(columns={"itemcode": "종목코드", "itemname": "종목명"})
etf=pd.merge(left=tickers,right=df,how='left',on='종목코드' )
etf
| 종목코드 | 종목명 | |
|---|---|---|
| 0 | 445690 | BNK 주주가치액티브 |
| 1 | 292340 | 마이티 200커버드콜ATM레버리지 |
| 2 | 442260 | 마이티 다이나믹퀀트액티브 |
| 3 | 159800 | 마이티 코스피100 |
| 4 | 361580 | KBSTAR 200TR |
| ... | ... | ... |
| 673 | 195980 | ARIRANG 신흥국MSCI(합성 H) |
| 674 | 433250 | UNICORN R&D 액티브 |
| 675 | 215620 | HK S&P코리아로우볼 |
| 676 | 391670 | HK 베스트일레븐액티브 |
| 677 | 391680 | HK 하이볼액티브 |
678 rows × 2 columns
총 678개의 ETF 티커명을 불러왔습니다.
주가 데이터 크롤링(일단위 OHLCV)
# df = pd.DataFrame(columns=['NAV','시가','고가','저가','종가','거래량','거래대금','기초지수','종목명','종목코드'])
# error_list = []
# for a, b in tqdm(etf[['종목명', '종목코드']].itertuples(index=False)):
# try:
# price = stock.get_etf_ohlcv_by_date("20100101", "20230309", b)
# price['종목명']=a
# price['종목코드']=b
# price = price.reset_index()
# df = pd.concat([df,price])
# except:
# error_list.append(a)
# time.sleep(1)
# etf_price = df.reset_index(drop=True)
# etf_price
데이터 필터링
#저장
#etf_price.to_pickle("../crawling/data/etf_price.pickle")
#불러오기
df = pd.read_pickle("../crawling/data/etf_price.pickle")
print("<<종목 수>>")
print("최초 :", df.종목코드.nunique())
# 필터링
black_str = ['레버리지','인버스','원유']
for black in black_str:
cond = df['종목명'].str.contains(black)
df = df[~cond]
print("레버리지 필터링 후 :",df.종목코드.nunique())
# 기간필터링
opendates = df.groupby("종목명")['날짜'].first().reset_index()
lastdates = df.groupby("종목명")['날짜'].last().reset_index()
lastdates.columns = ['종목명','날짜last']
oldates = pd.merge(opendates, lastdates, on='종목명')
cond = oldates['날짜']<'2017-01-01' ##### 2017년 이전 상장
new_oldates = oldates[cond]
new_list = new_oldates['종목명'].tolist()
cond = df['종목명'].isin(new_list)
etf_price = df[cond]
print("기간 필터링 후 :", etf_price.종목코드.nunique())
etf_price
<<종목 수>>
최초 : 678
레버리지 필터링 후 : 591
기간 필터링 후 : 168
| NAV | 시가 | 고가 | 저가 | 종가 | 거래량 | 거래대금 | 기초지수 | 종목명 | 종목코드 | 날짜 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 22631.83 | 22390 | 22585 | 22390 | 22550 | 58738 | 1325723895 | 223.49 | ACE 200 | 105190 | 2010-01-04 |
| 1 | 22566.21 | 22550 | 22725 | 22475 | 22555 | 47769 | 1081075485 | 222.84 | ACE 200 | 105190 | 2010-01-05 |
| 2 | 22748.91 | 22625 | 22735 | 22620 | 22715 | 74937 | 1701637315 | 224.67 | ACE 200 | 105190 | 2010-01-06 |
| 3 | 22409.69 | 22740 | 22740 | 22415 | 22455 | 26044 | 587893595 | 221.31 | ACE 200 | 105190 | 2010-01-07 |
| 4 | 22544.98 | 22365 | 22515 | 22230 | 22515 | 11803 | 264454100 | 222.66 | ACE 200 | 105190 | 2010-01-08 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020 | 9067.76 | 8915 | 9010 | 8850 | 8925 | 34137 | 304969115 | 978.07 | ARIRANG 신흥국MSCI(합성 H) | 195980 | 2023-03-08 |
| 2021 | 8937.23 | 8925 | 9035 | 8910 | 8955 | 22681 | 203142255 | 974.15 | ARIRANG 신흥국MSCI(합성 H) | 195980 | 2023-03-09 |
| 2025 | 12082.88 | 12040 | 12040 | 12040 | 12040 | 19 | 228760 | 9466.48 | HK S&P코리아로우볼 | 215620 | 2023-03-07 |
| 2026 | 11991.12 | 12035 | 12035 | 12020 | 12020 | 2 | 24055 | 9386.54 | HK S&P코리아로우볼 | 215620 | 2023-03-08 |
| 2027 | 12023.64 | 12040 | 12050 | 12040 | 12050 | 3 | 36140 | 9415.02 | HK S&P코리아로우볼 | 215620 | 2023-03-09 |
410997 rows × 11 columns
2. 샤프비율 최적화
데이터 변환
%%time
data = etf_price.pivot_table(index='날짜', columns='종목명', values='종가')
# 월말 데이터로 필터링
data= data.resample("M").last()
# 기간 필터링
data = data.loc[:"2023-02-28"]
data
CPU times: user 12 s, sys: 80 ms, total: 12.1 s
Wall time: 12.1 s
| 종목명 | ACE 200 | ACE Fn성장소비주도주 | ACE 국고채3년 | ACE 단기통안채 | ACE 미국다우존스리츠(합성 H) | ACE 밸류대형 | ACE 베트남VN30(합성) | ACE 삼성그룹동일가중 | ACE 삼성그룹섹터가중 | ACE 인도네시아MSCI(합성) | ... | TIGER 헬스케어 | TIGER 현대차그룹+펀더멘털 | TIGER 화장품 | TREX 200 | TREX 펀더멘탈 200 | 마이다스 200커버드콜5%OTM | 마이티 코스피100 | 파워 200 | 파워 고배당저변동성 | 파워 코스피100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 날짜 | |||||||||||||||||||||
| 2010-01-31 | 21240.0 | NaN | 102515.0 | NaN | NaN | NaN | NaN | NaN | 6505.0 | NaN | ... | NaN | NaN | NaN | 21190.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2010-02-28 | 21160.0 | NaN | 103350.0 | NaN | NaN | NaN | NaN | NaN | 6650.0 | NaN | ... | NaN | NaN | NaN | 21030.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2010-03-31 | 22485.0 | NaN | 103520.0 | NaN | NaN | NaN | NaN | NaN | 7035.0 | NaN | ... | NaN | NaN | NaN | 22415.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2010-04-30 | 22870.0 | NaN | 104545.0 | NaN | NaN | NaN | NaN | NaN | 7100.0 | NaN | ... | NaN | NaN | NaN | 22860.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2010-05-31 | 21385.0 | NaN | 104700.0 | NaN | NaN | NaN | NaN | NaN | 6690.0 | NaN | ... | NaN | NaN | NaN | 21465.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-10-31 | 30315.0 | 5305.0 | 100330.0 | 101175.0 | 76345.0 | 7810.0 | 16580.0 | 15385.0 | 15075.0 | 11500.0 | ... | 26945.0 | 20050.0 | 1745.0 | 30765.0 | 32485.0 | 11545.0 | 22885.0 | 30430.0 | 26585.0 | 22790.0 |
| 2022-11-30 | 32465.0 | 5900.0 | 102155.0 | 101430.0 | 79030.0 | 8365.0 | 15785.0 | 16080.0 | 15595.0 | 10785.0 | ... | 26840.0 | 21205.0 | 2110.0 | 32950.0 | 34875.0 | 12000.0 | 24385.0 | 32640.0 | 28590.0 | 24410.0 |
| 2022-12-31 | 29850.0 | 6175.0 | 101395.0 | 100145.0 | 75650.0 | 7860.0 | 15520.0 | 15600.0 | 14120.0 | 9845.0 | ... | 26210.0 | 19705.0 | 2335.0 | 30310.0 | 32665.0 | 11195.0 | 22500.0 | 29970.0 | 27610.0 | 22375.0 |
| 2023-01-31 | 32555.0 | 6515.0 | 102830.0 | 100485.0 | 81675.0 | 8480.0 | 16815.0 | 16265.0 | 15260.0 | 10040.0 | ... | 25995.0 | 21255.0 | 2470.0 | 32900.0 | 35135.0 | 12235.0 | 24555.0 | 32665.0 | 29000.0 | 24460.0 |
| 2023-02-28 | 32335.0 | 6500.0 | 101815.0 | 100715.0 | 78085.0 | 8420.0 | 16400.0 | 16025.0 | 15150.0 | 10485.0 | ... | 25220.0 | 22240.0 | 2400.0 | 32660.0 | 34880.0 | 12240.0 | 24450.0 | 32445.0 | 28725.0 | 24270.0 |
158 rows × 168 columns
행은 날짜로, 열을 종목명으로 구성된 종가 데이터프레임을 만듭니다.
print("상장일이 다르다보니, 종목별로 누락치가 많이 보입니다.")
print(data.isnull().sum())
상장일이 다르다보니, 종목별로 누락치가 많이 보입니다.
종목명
ACE 200 0
ACE Fn성장소비주도주 67
ACE 국고채3년 0
ACE 단기통안채 47
ACE 미국다우존스리츠(합성 H) 43
..
마이다스 200커버드콜5%OTM 13
마이티 코스피100 30
파워 200 25
파워 고배당저변동성 49
파워 코스피100 16
Length: 168, dtype: int64
임의 종목 선택(5개)
# 임의 종목 5개 선택
num=5
#tickers = np.random.choice(data.columns, num, replace=False) # replace=False : 중복없이
tickers = ['마이다스 200커버드콜5%OTM', 'TIGER 현대차그룹+펀더멘털', 'KBSTAR 우량업종','KBSTAR V&S셀렉트밸류', 'KODEX 철강']
print(tickers)
temp = data[tickers].dropna()
temp
['마이다스 200커버드콜5%OTM', 'TIGER 현대차그룹+펀더멘털', 'KBSTAR 우량업종', 'KBSTAR V&S셀렉트밸류', 'KODEX 철강']
| 종목명 | 마이다스 200커버드콜5%OTM | TIGER 현대차그룹+펀더멘털 | KBSTAR 우량업종 | KBSTAR V&S셀렉트밸류 | KODEX 철강 |
|---|---|---|---|---|---|
| 날짜 | |||||
| 2016-02-29 | 9870.0 | 17720.0 | 9360.0 | 10290.0 | 8495.0 |
| 2016-03-31 | 10260.0 | 18185.0 | 9520.0 | 10680.0 | 9025.0 |
| 2016-04-30 | 10280.0 | 18195.0 | 9570.0 | 10805.0 | 9540.0 |
| 2016-05-31 | 10170.0 | 17030.0 | 9420.0 | 10490.0 | 8300.0 |
| 2016-06-30 | 10165.0 | 16490.0 | 9155.0 | 10150.0 | 8225.0 |
| ... | ... | ... | ... | ... | ... |
| 2022-10-31 | 11545.0 | 20050.0 | 9775.0 | 11820.0 | 7430.0 |
| 2022-11-30 | 12000.0 | 21205.0 | 10675.0 | 12815.0 | 8475.0 |
| 2022-12-31 | 11195.0 | 19705.0 | 10225.0 | 12225.0 | 7805.0 |
| 2023-01-31 | 12235.0 | 21255.0 | 10665.0 | 13180.0 | 8310.0 |
| 2023-02-28 | 12240.0 | 22240.0 | 10555.0 | 13350.0 | 8735.0 |
85 rows × 5 columns
fig, (ax,ax2) = plt.subplots(nrows=2,
sharex=True,
figsize=(8,6))
cum_rets=((1+temp[13:].pct_change()).cumprod().fillna(1)-1)
cum_rets.plot(ax=ax, color=sns.color_palette("muted", 5))
ax.axhline(0, ls='--', color='black', lw=5, alpha=0.5)
ax.legend(loc='upper left')
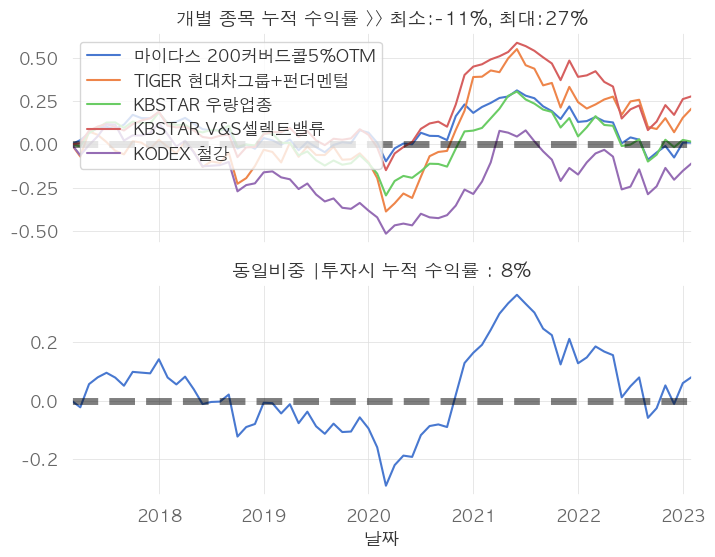
ax.set_title('개별 종목 누적 수익률 >> 최소:%d%%, 최대:%d%%'
% (cum_rets.iloc[-1,:].min()*100, cum_rets.iloc[-1,:].max()*100)
)
ew_cum_rets = (1+temp[13:].pct_change().fillna(0)).cumprod().sum(axis=1)/temp.shape[1] -1
ew_cum_rets.plot(ax=ax2, color=sns.color_palette("muted", 5))
ax2.axhline(0, ls='--', color='black', lw=5, alpha=0.5)
ax2.set_title('동일비중 |투자시 누적 수익률 : %d%%' % (100*ew_cum_rets[-1]))
샤프비율 최대화로 가중치 계산
샤프비율(Sharpe Ratio)은 투자 수익률과 그에 따른 위험을 평가하는 지표로, 특히 포트폴리오의 성과를 평가하는 데 자주 사용됩니다.
샤프비율은 다음과 같은 수식으로 계산됩니다.
Sharpe Ratio = (Rp - Rf) / σp
여기서 Rp는 포트폴리오의 예상 수익률, Rf는 무위험 이자율, σp는 포트폴리오의 수익률 표준편차를 나타냅니다.
샤프비율이 높을수록 같은 수익을 얻기 위해서는 더 적은 위험을 감수해야 함을 의미합니다. 따라서, 높은 샤프비율을 가진 포트폴리오가 보다 효율적인 투자 방식이라고 할 수 있습니다.
다음 코드는 포트폴리오 최적화를 위한 함수입니다.
입력으로 예상수익률(er)과 공분산(cov)이 주어지며,
목적함수로는 네거티브 샤프비율을 사용합니다.
최적화 방법으로 SLSQP를 사용하며,
가중치는 0과 1 사이 값으로 제약조건이 걸려 있습니다.
최적화 결과로 가중치(종목별 비중)를 반환합니다.
# 출처 : 퀀트대디
# 샤프비율 최대화 모델 가중치 계산 함수
def get_msr_weights(er, cov):
# 자산 개수
noa = er.shape[0]
# 초기 가중치
init_guess = np.repeat(1/noa, noa)
# 제약조건 및 상하한값
bounds = ((0.0, 1), ) * noa
weights_sum_to_1 = {'type' : 'eq',
'fun' : lambda weights:np.sum(weights)-1}
# 목적함수 : 네거티브 샤프비율
def neg_sharpe(weights, er, cov):
r = weights.T @ er
vol = np.sqrt(weights.T @ cov @ weights)
return -r / vol
# 최적화 수행
res = minimize(neg_sharpe,
init_guess,
args = (er, cov),
method = "SLSQP",
constraints = (weights_sum_to_1,),
bounds = bounds)
return res.x #가중치 결과
다음 코드는 12개월 롤링 기간으로 MSR(Maximize Sharpe Ratio) 전략을 적용하여 포트폴리오를 최적화하고 시각화하는 코드입니다.
주어진 종목들(tickers)의 수익률(rets)을 기반으로, 기대수익률(er)과 공분산(cov)을 계산합니다.
그 후, rolling 함수를 이용하여 12개월 단위로 공분산 행렬(cov)을 계산하고, 이를 이용해 get_msr_weights 함수를 적용하여 최적 가중치를 구합니다.
구해진 최적 가중치(msr_w_df)를 이용하여 포트폴리오 수익률(port_rets)을 계산하고 누적수익률(port_cum_rets)과 샤프 지수(port_sharpe)를 계산합니다.
최적화 결과(종목별 가중치)와 누적수익률을 시각화합니다.
# 수익률
rets = data[tickers].pct_change().dropna().fillna(0)
# 빈 데이터 프레임 생성
msr_w_df = pd.DataFrame().reindex_like(rets) #rets의 인덱스를 가져오는
# 기대수익률 배열
er = np.array(rets * 12)
pal = sns.color_palette("Spectral", len(tickers))
# 공분산행렬 배열
cov = rets.rolling(12).cov().fillna(0) * 12
# 공분산 행렬을 3차원 배열로 변환
cov = cov.values.reshape(int(cov.shape[0] / cov.shape[1]), cov.shape[1], cov.shape[1])
for i in range(12, len(msr_w_df)): # 처음 12개월은 값이 없음. cov계산에 사용되어있어서
msr_w_df.iloc[i] = get_msr_weights(er[i-1], cov[i-1])
# 포트폴리오 수익률 데이터프레임
port_rets = msr_w_df.shift() * rets
port_cum_rets = (1+port_rets.sum(axis=1)).cumprod() - 1
port_sharpe = port_rets.sum(axis=1).mean()*12 / (port_rets.sum(axis=1).std()*np.sqrt(12))
# 시각화
fig, ax = plt.subplots(figsize=(8,5))
ax.stackplot(msr_w_df.index, msr_w_df.T, labels=msr_w_df.columns, colors=pal)
ax.legend(loc='upper left')
ax.set_title('12개월 롤링 샤프지수 최대화 누적수익률 : %d%%' % (100*port_cum_rets[-1]) )
ax.set_xlabel("Date")
ax.set_ylabel("Weights")
ax2 = ax.twinx()
ax2.plot(port_cum_rets, lw=2, c='blue')#, ls='--')
ax2.axhline(0, color='black', alpha=0.5, ls='--')
ax.set_xlim(datetime.date(2016,11,29), datetime.date(2023,3,1))
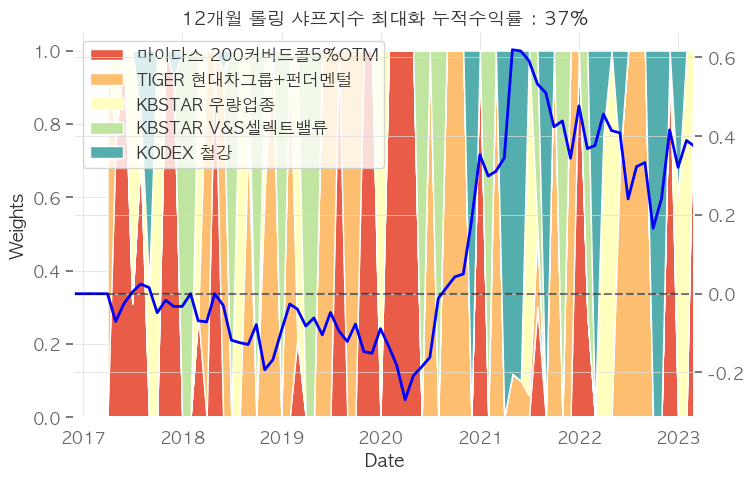
세로 좌측 : 투자비중, 세로 우측 : 누적수익률
투자기간 5년동안 종목 비중을 월마다 리밸런싱해주는 것이
개별종목 최대 수익률(27%)보다보다 더 높은 수익률(37%)을 보여주지만,
안정적으로 보이진 않습니다.
실제로 랜덤으로 5종목을 뽑으면 성과가 매우 안 좋았습니다.
설명을 위해 위 종목을 선정하였습니다.
3. 종목선택 : 몬테카를로 시뮬레이션
임의로 종목5개씩 시나리오 1000번 시뮬레이션
다음 코드는 포트폴리오 최적화를 구현한 것입니다.
먼저, 시뮬레이션을 실행하기 위한 변수(cnt, num_of_tickers, rolling_window, threshold)를 설정합니다. 이후, 상관관계(coefficient)가 threshold보다 높은 티커들을 필터링하여 common_tickers에 저장합니다.
그 다음, cnt번 시뮬레이션을 반복하여 다음의 작업을 수행합니다.
- common_tickers와 random_tickers(상관관계가 threshold보다 낮은 티커들)에서 num_of_tickers개의 티커를 선택하여 tickers 리스트에 저장합니다.
- tickers 리스트에 해당하는 종목들의 수익률을 계산하여 rets에 저장합니다.
- rets에 대해 MSR을 수행하여 최적의 포트폴리오 비중을 계산하고, 이를 msr_w_df에 저장합니다.
- msr_w_df와 rets를 곱하여 포트폴리오 수익률을 계산하고, 이를 이용하여 누적 수익률(port_cum_rets), 12개월 수익률(ret_12m), Sharpe Ratio(port_sharpe)를 계산합니다.
- 포트폴리오 티커(tickers), 누적 수익률(port_cum_rets[-1]), 12개월 수익률(ret_12m[-1]), Sharpe Ratio(port_sharpe)를 각각 리스트(port, ret, ret_12m, sharpe)에 저장합니다. 또한, 현재까지의 최고 누적 수익률(top)과 비교하여 더 높은 수익률을 얻은 경우에는 이를 갱신하고, 이에 따른 정보를 출력합니다.
port = []
ret = []
ret_12m = []
sharpe = []
########################################
cnt = 1000 #시나리오 개수
num_of_tickers = 5 # 종목개수
rolling_window = 12 # 롤링윈도우
# common_tickers의 종목과 상관계수가 0.7 이상인 ticker들 필터링
threshold = 0.7 #상관계수 필터링 조건
common_tickers = [] #
########################################
ticker_list = data.columns.tolist()
for ticker in common_tickers:
temp = data.corr()[ticker]
high_corr_tickers = temp[temp>threshold].index.tolist()
ticker_list = [i for i in ticker_list if i not in high_corr_tickers]
random_tickers = ticker_list.copy()
print(num_of_tickers, threshold, len(random_tickers))
for _ in tqdm(range(cnt)):
tickers = common_tickers + np.random.choice(random_tickers, num_of_tickers-len(common_tickers), False).tolist() # False: 중복비허용
# 수익률
rets = data[tickers].pct_change().dropna().fillna(0) #최근 있는 데이터로만 모델링
# 빈 데이터 프레임 생성
msr_w_df = pd.DataFrame().reindex_like(rets) #rets의 인덱스를 가져오는
# 기대수익률 배열
er = np.array(rets * 12)
# 공분산행렬 배열
cov = rets.rolling(12).cov().fillna(0) * 12
# 공분산 행렬을 3차원 배열로 변환
cov = cov.values.reshape(int(cov.shape[0] / cov.shape[1]), cov.shape[1], cov.shape[1])
for i in range(rolling_window, len(msr_w_df)): # 처음 12개월은 값이 없음. cov계산에 사용되어있어서
msr_w_df.iloc[i] = get_msr_weights(er[i-1], cov[i-1])
# 포트폴리오 수익률 데이터프레임
port_rets = msr_w_df.shift() * rets
port_cum_rets = (1+port_rets.sum(axis=1)).cumprod() - 1
port_sharpe = port_rets.sum(axis=1).mean()*12 / (port_rets.sum(axis=1).std()*np.sqrt(12))
#port_cum_rets.plot()
port.append(tickers)
ret.append(port_cum_rets[-1])
ret_12m.append((port_rets.sum(axis=1)[-12:]+1).cumprod()[-1]-1)
sharpe.append(port_sharpe)
# 최고값 초기화
if _==0:
top = ret[-1]
if ret[-1] > top:
print(port_cum_rets[-1].round(2), ret_12m[-1].round(2), port_sharpe.round(2), tickers)
top = ret[-1]
results = pd.DataFrame({"port":port,"ret":ret,"ret_12m":ret_12m,"sharpe":sharpe})
cond = results['ret'] > 1
results = results[cond].sort_values(by='sharpe', ascending=False)
results[:10]
| port | ret | ret_12m | sharpe | |
|---|---|---|---|---|
| 949 | [TIGER LG그룹+펀더멘털, ARIRANG 미국다우존스고배당주(합성 H), KO... | 1.083995 | 0.105965 | 1.032625 |
| 325 | [TIGER 200 IT, ACE 밸류대형, KODEX 200, KODEX 미국달러... | 1.041779 | 0.091459 | 0.838990 |
| 145 | [KODEX 배당성장, TIGER 미국나스닥100, TIGER KTOP30, KOS... | 1.094986 | 0.068243 | 0.830157 |
| 134 | [ARIRANG 코스피50, ARIRANG 코스피, KODEX 일본TOPIX100,... | 1.134787 | 0.170098 | 0.769744 |
| 507 | [ACE 코스닥(합성), KOSEF 미국달러선물, KODEX 반도체, TIGER 유... | 1.004255 | 0.045385 | 0.768535 |
| 84 | [KODEX 삼성그룹, TREX 200, TIGER S&P글로벌헬스케어(합성), 파... | 1.042702 | 0.095163 | 0.755316 |
| 490 | [KODEX 미국S&P500산업재(합성), ACE 중국본토CSI300, TIGER ... | 1.131652 | 0.202374 | 0.752559 |
| 220 | [TIGER 200 중공업, TIGER 200 금융, TIGER 단기선진하이일드(합... | 1.275585 | 0.376153 | 0.725623 |
| 213 | [KODEX 반도체, TIGER 200 IT, KOSEF 미국달러선물, KOSEF ... | 1.729249 | 0.035973 | 0.720899 |
| 174 | [KOSEF 블루칩, KODEX 코스닥150, TIGER 미국나스닥100, TIGE... | 1.109075 | -0.305920 | 0.644526 |
상위 3개의 결과 시각화
idxs = results[:3].index.tolist()
for idx in idxs:
tickers = results.loc[idx]['port']
print(idx, tickers)
# 수익률
rets = data[tickers].pct_change().dropna().fillna(0)
# 팔레트
pal = sns.color_palette("Spectral", len(tickers))
# 빈 데이터 프레임 생성
msr_w_df = pd.DataFrame().reindex_like(rets) #rets의 인덱스를 가져오는
# 기대수익률 배열
er = np.array(rets * 12)
# 공분산행렬 배열
cov = rets.rolling(12).cov().fillna(0) * 12
# 공분산 행렬을 3차원 배열로 변환
cov = cov.values.reshape(int(cov.shape[0] / cov.shape[1]), cov.shape[1], cov.shape[1])
for i in range(12, len(msr_w_df)): # 처음 12개월은 값이 없음. cov계산에 사용되어있어서
msr_w_df.iloc[i] = get_msr_weights(er[i-1], cov[i-1])
# 포트폴리오 수익률 데이터프레임
port_rets = msr_w_df.shift() * rets
port_cum_rets = (1+port_rets.sum(axis=1)).cumprod() - 1
# 시각화
fig, ax = plt.subplots(figsize=(8,5))
ax.stackplot(msr_w_df.index, msr_w_df.T, labels=msr_w_df.columns, colors=pal)
ax.legend(loc='upper left')
ax.set_title(f"{idx} {tickers }MSR Weights", fontsize=8)
ax.set_xlabel("Date")
ax.set_ylabel("Weights")
ax2 = ax.twinx()
ax2.plot(port_cum_rets, lw=1, c='black')#, ls='--')
949 ['TIGER LG그룹+펀더멘털', 'ARIRANG 미국다우존스고배당주(합성 H)', 'KODEX 미국달러선물', 'TIGER 단기선진하이일드(합성 H)', 'TIGER 200 IT']
325 ['TIGER 200 IT', 'ACE 밸류대형', 'KODEX 200', 'KODEX 미국달러선물', 'KODEX 바이오']
145 ['KODEX 배당성장', 'TIGER 미국나스닥100', 'TIGER KTOP30', 'KOSEF 미국달러선물', 'TIGER 코스닥150']
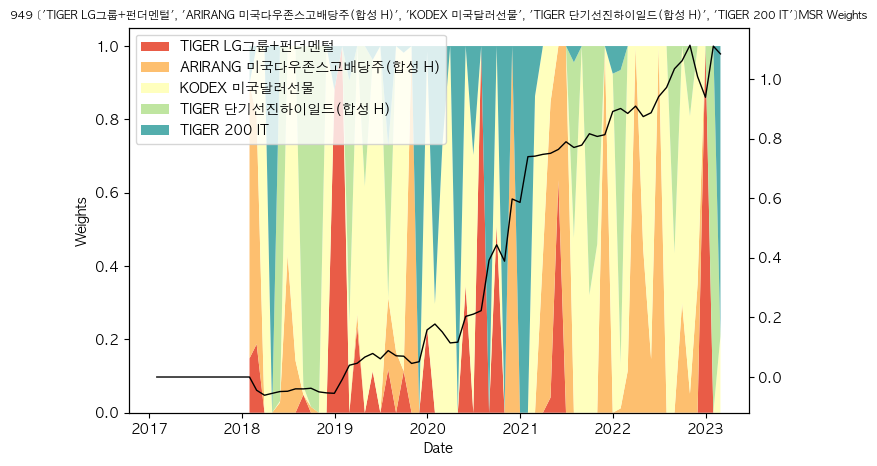
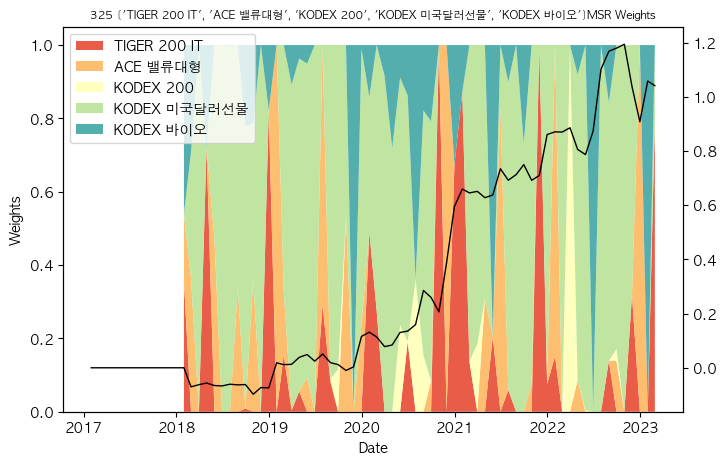
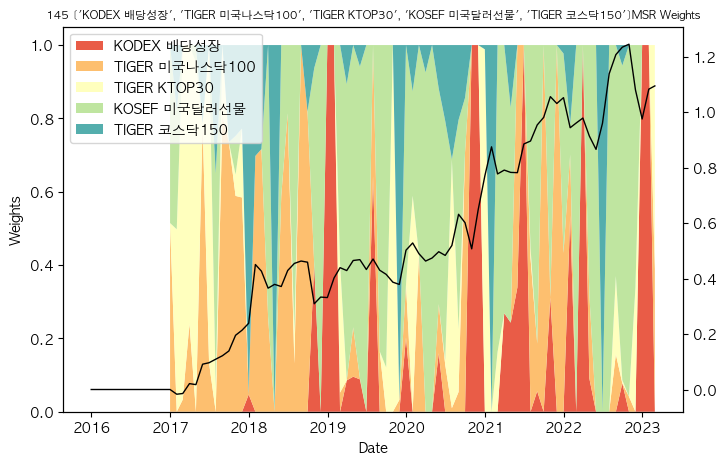
1000번의 시뮬레이션해도 결과가 신통치 않습니다.
모든 경우의 수를 다 해본다면 좋겠지만, 해를 개선해 나가기 위한 방법이 필요합니다.
대안으로 다음을 생각합니다.
- 종목 몇개를 고정하고, 상관계수가 높은 종목들을 필터링해주기
- 유전알고리즘으로 종목 선택 개선하기
4. 종목선택 : 유전알고리즘
다음 코드는 주식 선택을 위한 유전 알고리즘입니다. 먼저 세대 수, 짝짓기하는 부모 수, 모집단 크기, 돌연변이율, 적합도 함수와 같은 유전 알고리즘 파라미터를 설정합니다.
그런 다음 포트폴리오에 포함할 종목을 무작위로 선택해 모집단을 초기화합니다.
그런 다음 선택한 종목에 대한 기대 수익률과 공분산 행렬을 계산하는 적합도 함수를 정의하고 최대 샤프 비율(MSR) 포트폴리오의 가중치를 계산합니다.
MSR 포트폴리오는 무위험 수익률 대비 초과 수익률을 포트폴리오의 표준 편차로 나눈 값인 샤프 비율을 최대화하는 포트폴리오입니다.
그런 다음 알고리즘은 지정된 세대 수 동안 실행되며, 각 세대마다 적합성 점수를 기준으로 가장 적합한 부모를 선택하고, 교차 및 돌연변이를 수행하여 새로운 자손을 생성하고, 적합성 점수를 평가합니다.
그런 다음 적합성 점수가 가장 높은 자손을 모집단에 추가하고 지정된 세대 수에 도달할 때까지 이 과정을 반복합니다.
이 코드에는 각 세대에 대해 최고의 적합성 점수와 해당 티커 기호를 인쇄하는 콜백 함수도 있습니다. 알고리즘이 끝나면 최적의 솔루션(즉, 적합도 점수가 가장 높은 포트폴리오)이 반환됩니다.
import pygad
##### hypter parameter
tic = time.time()
# 유전자집합
#ticker_list = data.columns.tolist()
num_select_stocks = 5
pal = sns.color_palette("Spectral", num_select_stocks)
print("유전자집합 :", len(ticker_list))
print("유전자개수 :", num_select_stocks)
print("common_tickers :", common_tickers)
print('-'*100)
def fitness_func(solution, solution_idx):
#global tickers
tickers = [ticker_list[i] for i in solution]+common_tickers
# 수익률
rets = data[tickers].pct_change().dropna().fillna(0)
# 빈 데이터 프레임 생성
msr_w_df = pd.DataFrame().reindex_like(rets) #rets의 인덱스를 가져오는
# 기대수익률 배열
er = np.array(rets * 12)
# 공분산행렬 배열
cov = rets.rolling(12).cov().fillna(0) * 12
# 공분산 행렬을 3차원 배열로 변환
cov = cov.values.reshape(int(cov.shape[0] / cov.shape[1]), cov.shape[1], cov.shape[1])
for i in range(12, len(msr_w_df)): # 처음 12개월은 값이 없음. cov계산에 사용되어있어서
msr_w_df.iloc[i] = get_msr_weights(er[i-1], cov[i-1])
# 포트폴리오 수익률 데이터프레임
port_rets = msr_w_df.shift() * rets
port_cum_rets = (1+port_rets.sum(axis=1)).cumprod() - 1
port_sharpe = port_rets.sum(axis=1).mean()*12 / (port_rets.sum(axis=1).std()*np.sqrt(12))
# print((1+port_rets.sum(axis=1)).cumprod()[-1])
# print('-'*30)
return (1+port_rets.sum(axis=1)).cumprod()[-1]-1 # 최대화
fitness_function = fitness_func
num_generations = 15 # Number of generations.
num_parents_mating = 5 # Number of solutions to be selected as parents in the mating pool.
# To prepare the initial population, there are 2 ways:
# 1) Prepare it yourself and pass it to the initial_population parameter. This way is useful when the user wants to start the genetic algorithm with a custom initial population.
# 2) Assign valid integer values to the sol_per_pop and num_genes parameters. If the initial_population parameter exists, then the sol_per_pop and num_genes parameters are useless.
sol_per_pop = 30 # Number of solutions in the population.
num_genes = num_select_stocks-len(common_tickers) #5
init_range_low = 0
init_range_high = data[ticker_list].shape[1]-1
parent_selection_type = "sss" # Type of parent selection. sss (for steady-state selection), rws (for roulette wheel selection), sus (for stochastic universal selection), rank (for rank selection), random (for random selection), and tournament (for tournament selection)
keep_parents = 1 # Number of parents to keep in the next population. -1 means keep all parents and 0 means keep nothing.
crossover_type = "single_point" # Type of the crossover operator.
# Parameters of the mutation operation.
mutation_type = 'random' # Type of the mutation operator.
mutation_percent_genes = 80 # Percentage of genes to mutate. This parameter has no action if the parameter mutation_num_genes exists or when mutation_type is None.
last_fitness = 0
def callback_generation(ga_instance):
global last_fitness
global tickers
tickers = [ticker_list[i] for i in ga_instance.best_solution()[0]]+common_tickers
print("Generation = [{generation}]".format(generation=ga_instance.generations_completed), "\tFitness = {fitness}".format(fitness=ga_instance.best_solution()[1].round(4)), "\t Best tickers = {tickers}".format(tickers = [ticker_list[i] for i in ga_instance.best_solution()[0]]+common_tickers))
# print("Best tickers = {tickers}".format(tickers = [ticker_list[i] for i in ga_instance.best_solution()[0]]+common_tickers))
print('-'*100)
#print("Change = {change}".format(change=ga_instance.best_solution()[1] - last_fitness))
last_fitness = ga_instance.best_solution()[1]
initial_population = [] # 없음
# Creating an instance of the GA class inside the ga module. Some parameters are initialized within the constructor.
if len(initial_population) > 0 :
print('initial_population')
ga_instance = pygad.GA(initial_population=initial_population, # 초기 집단 설정
num_generations=num_generations,
num_parents_mating=num_parents_mating,
fitness_func=fitness_function,
sol_per_pop=sol_per_pop,
num_genes=num_genes,
init_range_low=init_range_low,
init_range_high=init_range_high,
parent_selection_type=parent_selection_type,
keep_parents=keep_parents,
crossover_type=crossover_type,
mutation_type=mutation_type,
mutation_percent_genes=mutation_percent_genes,
on_generation=callback_generation,
gene_type=int, #좀옥을 선택하는 것으니 int로
save_best_solutions=True)
else:
ga_instance = pygad.GA(
num_generations=num_generations,
num_parents_mating=num_parents_mating,
fitness_func=fitness_function,
sol_per_pop=sol_per_pop,
num_genes=num_genes,
init_range_low=init_range_low,
init_range_high=init_range_high,
parent_selection_type=parent_selection_type,
keep_parents=keep_parents,
crossover_type=crossover_type,
mutation_type=mutation_type,
mutation_percent_genes=mutation_percent_genes,
on_generation=callback_generation,
gene_type=int, #좀옥을 선택하는 것으니 int로
save_best_solutions=True)
# Running the GA to optimize the parameters of the function.
ga_instance.run()
# After the generations complete, some plots are showed that summarize the how the outputs/fitenss values evolve over generations.
ga_instance.plot_result()
# Returning the details of the best solution.
solution, solution_fitness, solution_idx = ga_instance.best_solution()
print("Parameters of the best solution : {solution}".format(solution=solution))
print("Fitness value of the best solution = {solution_fitness}".format(solution_fitness=solution_fitness))
print("Index of the best solution : {solution_idx}".format(solution_idx=solution_idx))
# prediction = numpy.sum(numpy.array(function_inputs)*solution)
# print("Predicted output based on the best solution : {prediction}".format(prediction=prediction))
if ga_instance.best_solution_generation != -1:
print("Best fitness value reached after {best_solution_generation} generations.".format(best_solution_generation=ga_instance.best_solution_generation))
# Saving the GA instance.
filename = 'genetic' # The filename to which the instance is saved. The name is without extension.
ga_instance.save(filename=filename)
# Loading the saved GA instance.
#loaded_ga_instance = pygad.load(filename=filename)
#loaded_ga_instance.run()
#loaded_ga_instance.plot_result()
#solution, solution_fitness, solution_idx = loaded_ga_instance.best_solution()
print(time.time()-tic,"seconds")
solution
유전자집합 : 146
유전자개수 : 5
common_tickers : []
----------------------------------------------------------------------------------------------------
Generation = [1] Fitness = 0.7765 Best tickers = ['KBSTAR 5대그룹주', 'TIGER 코스닥150바이오테크', 'KODEX 미국달러선물', 'KODEX 200', 'ACE 미국다우존스리츠(합성 H)']
----------------------------------------------------------------------------------------------------
Generation = [2] Fitness = 0.8345 Best tickers = ['ACE Fn성장소비주도주', 'TIGER 200 에너지화학', 'KODEX 미국달러선물', 'KODEX 200', 'ACE Fn성장소비주도주']
----------------------------------------------------------------------------------------------------
Generation = [3] Fitness = 1.0922 Best tickers = ['KODEX 건설', 'TIGER 우량가치', '마이티 코스피100', 'KODEX 미국S&P500에너지(합성)', 'ACE 미국다우존스리츠(합성 H)']
----------------------------------------------------------------------------------------------------
Generation = [4] Fitness = 1.7465 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', '마이다스 200커버드콜5%OTM', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [5] Fitness = 1.7465 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', '마이다스 200커버드콜5%OTM', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [6] Fitness = 1.9916 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 펀더멘탈 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [7] Fitness = 1.9916 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 펀더멘탈 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [8] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [9] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [10] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [11] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [12] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [13] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [14] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
Generation = [15] Fitness = 2.2685 Best tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
----------------------------------------------------------------------------------------------------
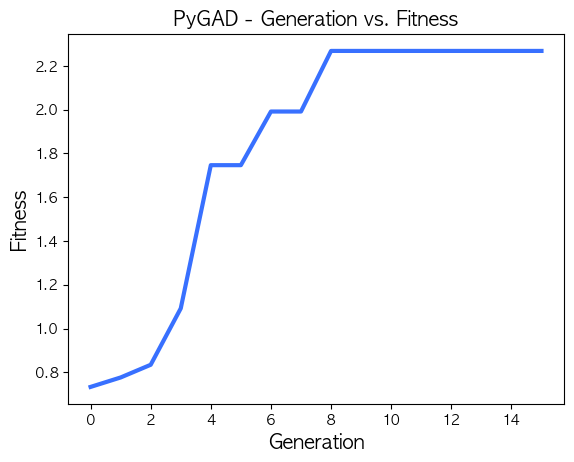
Parameters of the best solution : [ 23 132 139 85 78]
Fitness value of the best solution = 2.268480819777148
Index of the best solution : 0
Best fitness value reached after 8 generations.
246.91905093193054 seconds
#tickers = [ticker_list[i] for i in solution] + common_tickers
tickers = ['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
print(tickers)
# 수익률
rets = data[tickers].pct_change().dropna().fillna(0)
pal = sns.color_palette("Spectral", len(tickers))
# 빈 데이터 프레임 생성
msr_w_df = pd.DataFrame().reindex_like(rets) #rets의 인덱스를 가져오는
# 기대수익률 배열
er = np.array(rets * 12)
# 공분산행렬 배열
cov = rets.rolling(12).cov().fillna(0) * 12
# 공분산 행렬을 3차원 배열로 변환
cov = cov.values.reshape(int(cov.shape[0] / cov.shape[1]), cov.shape[1], cov.shape[1])
for i in range(12, len(msr_w_df)): # 처음 12개월은 값이 없음. cov계산에 사용되어있어서
msr_w_df.iloc[i] = get_msr_weights(er[i-1], cov[i-1])
# 포트폴리오 수익률 데이터프레임
port_rets = msr_w_df.shift() * rets
port_cum_rets = (1+port_rets.sum(axis=1)).cumprod() - 1
port_sharpe = port_rets.sum(axis=1).mean()*12 / (port_rets.sum(axis=1).std()*np.sqrt(12))
# 시각화
fig, ax = plt.subplots(figsize=(8,5))
ax.stackplot(msr_w_df.index, msr_w_df.T, labels=msr_w_df.columns, colors=pal)
ax.legend(loc='upper left')
ax.set_title("MSR Weights and Cummulative Returns")
ax.set_xlabel("Date")
ax.set_ylabel("Weights")
ax2 = ax.twinx()
ax2.plot(port_cum_rets, lw=2, c='blue')#, ls='--')
print(((1+port_rets.sum(axis=1)).cumprod()[-1]-1).round(2), ((1+port_rets.sum(axis=1)[-12:]).cumprod()[-1]-1).round(2), port_sharpe.round(2))
['KBSTAR 200', 'TIGER 코스닥150', 'TREX 200', 'TIGER 200 IT', 'KOSEF 미국달러선물']
2.27 0.22 1.13
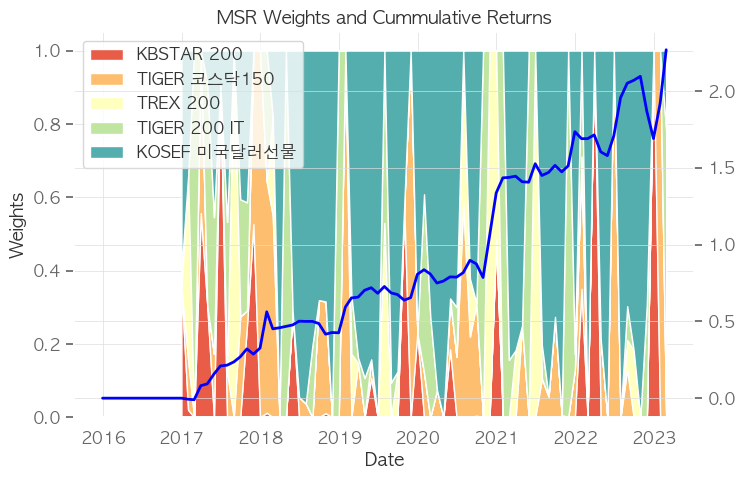
# 그림 사이즈 지정
fig, ax = plt.subplots( figsize=(5,5) )
# 삼각형 마스크를 만든다(위 쪽 삼각형에 True, 아래 삼각형에 False)
mask = np.zeros_like(data[tickers].corr(), dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# 히트맵을 그린다
sns.heatmap(data[tickers].corr(),
cmap = 'RdYlBu_r',
annot = True, # 실제 값을 표시한다
mask=mask, # 표시하지 않을 마스크 부분을 지정한다
linewidths=.5, # 경계면 실선으로 구분하기
cbar_kws={"shrink": .5},# 컬러바 크기 절반으로 줄이기
vmin = -1,vmax = 1 # 컬러바 범위 -1 ~ 1
)
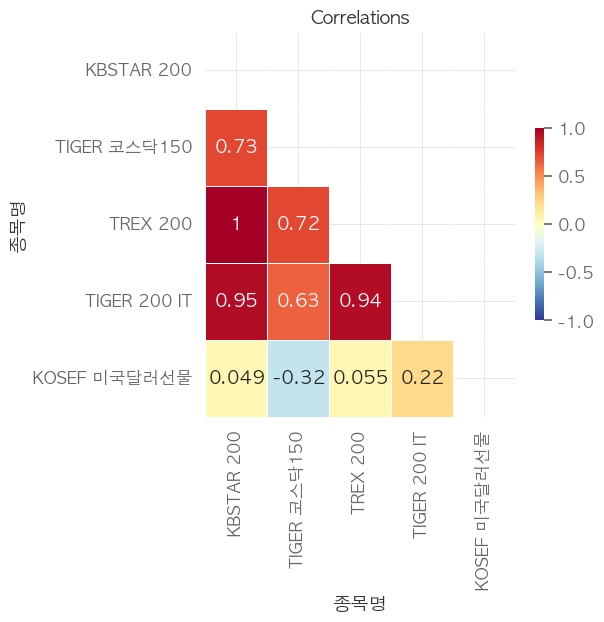
ax.set_title("Correlations")
plt.show()
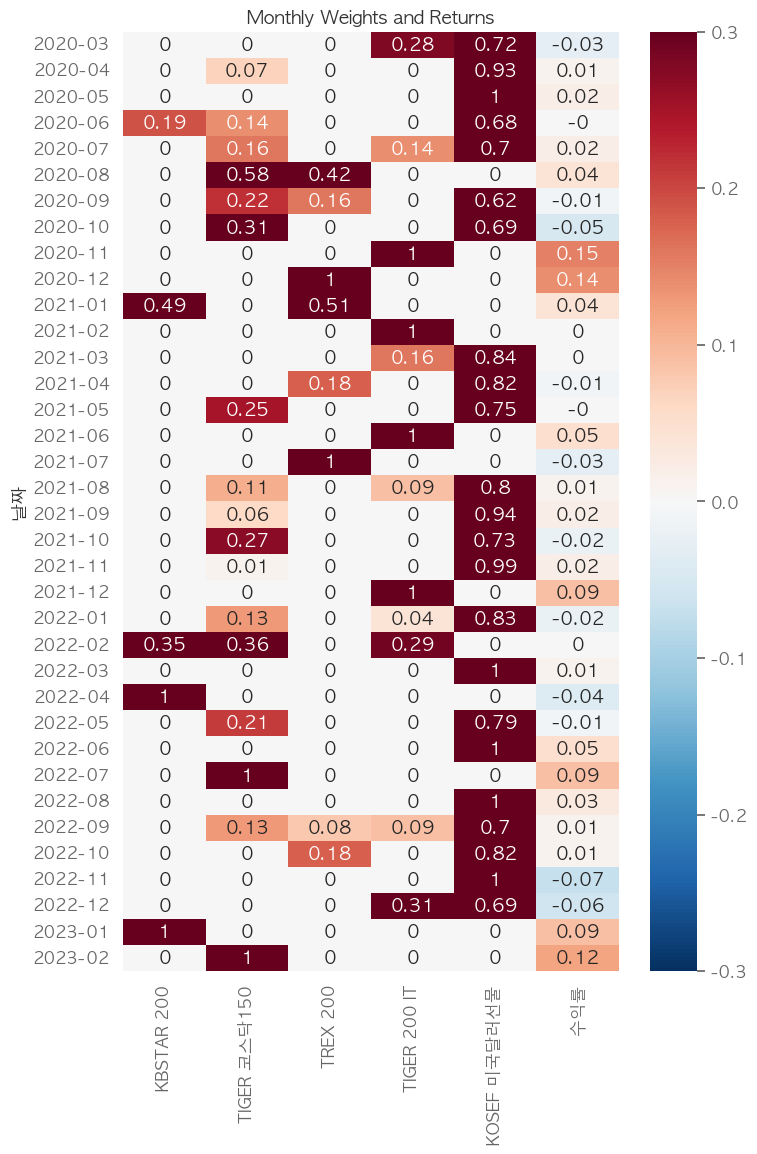
# 시뮬레이션 투자비중, 수익률
periods=36
fig, ax = plt.subplots(figsize=(8,5+periods*0.2))
weights = msr_w_df.shift().iloc[-periods:].reset_index()
returns = pd.DataFrame(port_rets.sum(axis=1), columns=['수익률']).reset_index()
temp = pd.merge(weights, returns, on='날짜', how='inner').set_index("날짜")
sns.heatmap(temp.round(2), cmap='RdBu_r', vmin=-0.3, vmax=0.3, annot=True, ax=ax)
ax.set_yticklabels(weights.날짜.apply(lambda x:x.strftime("%Y-%m")))
ax.set_title("Monthly Weights and Returns")
;
benchmark = qs.utils.download_returns("SPY")
benchmark = benchmark.tz_convert(None)
# 슬리피지 0.001 : 리밸런싱 수수료 등을 포함한 손실
qs.reports.basic((port_rets.sum(axis=1)-0.001).iloc[12:], benchmark=benchmark, periods_per_year=12, match_dates=True)
Performance Metrics
Strategy Benchmark
------------------ ---------- -----------
Start Period 2017-01-31 2017-01-31
End Period 2023-02-28 2023-02-28
Risk-Free Rate 0.0% 0.0%
Time in Market 100.0% 100.0%
Cumulative Return 203.86% 95.34%
CAGR﹪ 20.06% 11.64%
Sharpe 1.17 0.72
Prob. Sharpe Ratio 99.98% 95.07%
Sortino 2.93 1.06
Sortino/√2 2.07 0.75
Omega 2.87 2.87
Max Drawdown -13.28% -23.93%
Longest DD Days 337 393
Gain/Pain Ratio 1.87 0.69
Gain/Pain (1M) 1.87 0.69
Payoff Ratio 1.41 0.69
Profit Factor 2.87 1.69
Common Sense Ratio 7.05 1.65
CPC Index 2.52 0.81
Tail Ratio 2.45 0.98
Outlier Win Ratio 3.27 3.63
Outlier Loss Ratio 4.01 1.82
MTD 11.83% -2.51%
3M 5.17% 3.07%
6M 9.83% -2.69%
YTD 21.28% 4.05%
1Y 19.98% -10.5%
3Y (ann.) 21.03% 10.7%
5Y (ann.) 16.53% 9.87%
10Y (ann.) 20.06% 11.64%
All-time (ann.) 20.06% 11.64%
Avg. Drawdown -5.12% -9.43%
Avg. Drawdown Days 117 121
Recovery Factor 15.35 3.98
Ulcer Index 0.04 0.08
Serenity Index 33.77 4.36
Strategy Visualization
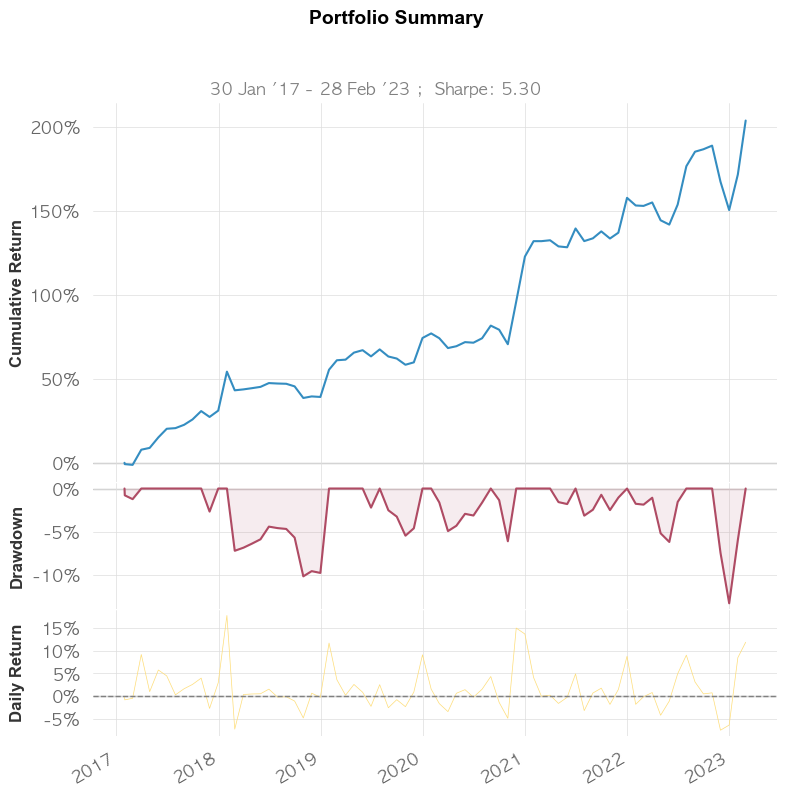
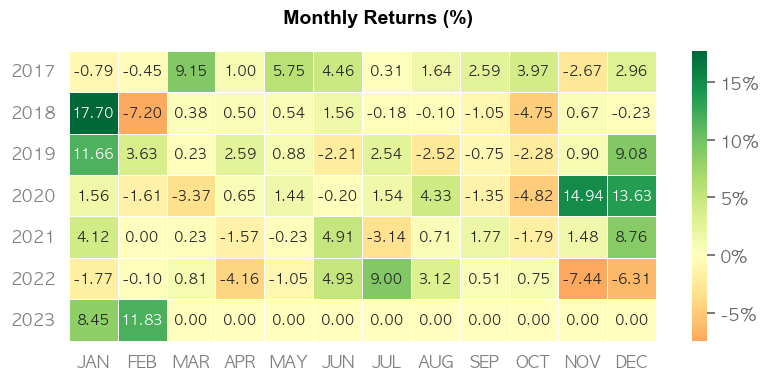
포트폴리오 누적 수익률은 224%(슬리피지 반영으로 226%보다 낮아졌습니다)로 랜덤수익률 108%, S&P500의 95% 누적수익률보다 높습니다. 다만, 달러를 제외하고 나머지 자산들의 상관성이 너무 높습니다.(붉은색)
5. 최종 시뮬레이션 결과 시각화
유전알고리즘으로 몇번 더 돌려보고, 직접 종목을 개선해 나갔습니다.
여러번의 시뮬레이션을 거쳐 가장 좋은 수익률을 낸 종목 5개를 선택합니다.
#tickers = [ticker_list[i] for i in solution] + common_tickers
tickers = ['KOSEF 미국달러선물',
'KODEX 미국S&P500산업재(합성)',
'TIGER 200 IT',
'TIGER 200 에너지화학',
'TIGER 코스닥150']
print(tickers)
# 수익률
rets = data[tickers].pct_change().dropna().fillna(0)
pal = sns.color_palette("Spectral", len(tickers))
# 빈 데이터 프레임 생성
msr_w_df = pd.DataFrame().reindex_like(rets) #rets의 인덱스를 가져오는
# 기대수익률 배열
er = np.array(rets * 12)
# 공분산행렬 배열
cov = rets.rolling(12).cov().fillna(0) * 12
# 공분산 행렬을 3차원 배열로 변환
cov = cov.values.reshape(int(cov.shape[0] / cov.shape[1]), cov.shape[1], cov.shape[1])
for i in range(12, len(msr_w_df)): # 처음 12개월은 값이 없음. cov계산에 사용되어있어서
msr_w_df.iloc[i] = get_msr_weights(er[i-1], cov[i-1])
# 포트폴리오 수익률 데이터프레임
port_rets = msr_w_df.shift() * rets
port_cum_rets = (1+port_rets.sum(axis=1)).cumprod() - 1
port_sharpe = port_rets.sum(axis=1).mean()*12 / (port_rets.sum(axis=1).std()*np.sqrt(12))
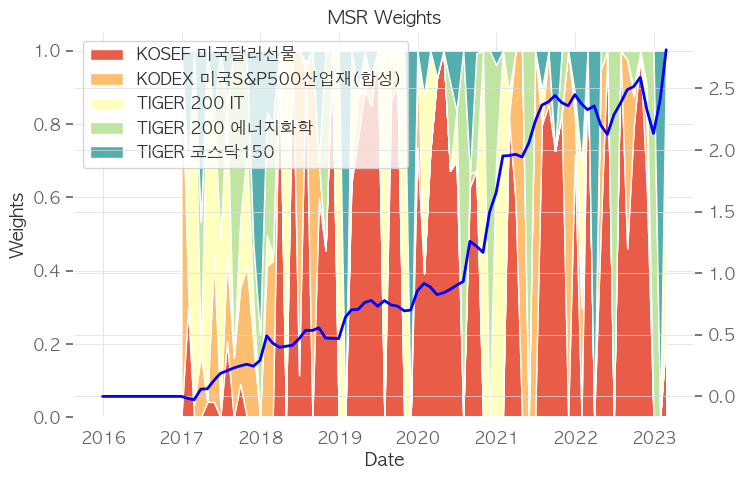
# 시각화
fig, ax = plt.subplots(figsize=(8,5))
ax.stackplot(msr_w_df.index, msr_w_df.T, labels=msr_w_df.columns, colors=pal)
ax.legend(loc='upper left')
ax.set_title("MSR Weights")
ax.set_xlabel("Date")
ax.set_ylabel("Weights")
ax2 = ax.twinx()
ax2.plot(port_cum_rets, lw=2, c='blue')#, ls='--')
print(((1+port_rets.sum(axis=1)).cumprod()[-1]-1).round(2), ((1+port_rets.sum(axis=1)[-12:]).cumprod()[-1]-1).round(2), port_sharpe.round(2))
['KOSEF 미국달러선물', 'KODEX 미국S&P500산업재(합성)', 'TIGER 200 IT', 'TIGER 200 에너지화학', 'TIGER 코스닥150']
2.81 0.15 1.27
상관관계
# 그림 사이즈 지정
fig, ax = plt.subplots( figsize=(5,5) )
# 삼각형 마스크를 만든다(위 쪽 삼각형에 True, 아래 삼각형에 False)
mask = np.zeros_like(data[tickers].corr(), dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# 히트맵을 그린다
sns.heatmap(data[tickers].corr(),
cmap = 'RdYlBu_r',
annot = True, # 실제 값을 표시한다
mask=mask, # 표시하지 않을 마스크 부분을 지정한다
linewidths=.5, # 경계면 실선으로 구분하기
cbar_kws={"shrink": .5},# 컬러바 크기 절반으로 줄이기
vmin = -1,vmax = 1 # 컬러바 범위 -1 ~ 1
)
plt.show()
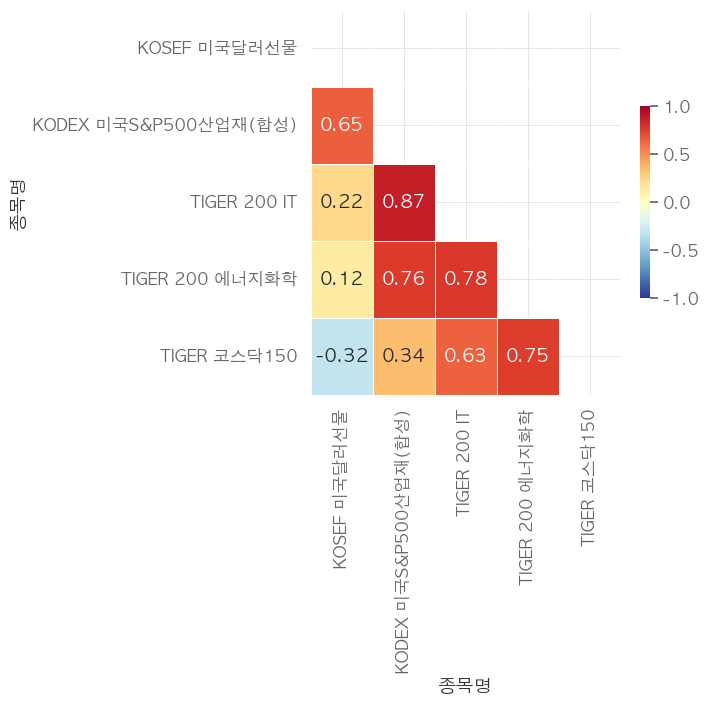
역시나 달러를 제외하고는 상관계수가 조금 높은 편입니다. 좋은 포트폴리오라고 보기엔 어려울 것 같습니다.
투자비중
# 시뮬레이션 투자비중, 수익률
periods=36
fig, ax = plt.subplots(figsize=(8,5+periods*0.2))
weights = msr_w_df.shift().iloc[-periods:].reset_index()
returns = pd.DataFrame(port_rets.sum(axis=1), columns=['수익률']).reset_index()
temp = pd.merge(weights, returns, on='날짜', how='inner').set_index("날짜")
sns.heatmap(temp.round(2), cmap='RdBu_r', vmin=-0.3, vmax=0.3, annot=True, ax=ax)
ax.set_yticklabels(weights.날짜.apply(lambda x:x.strftime("%Y-%m")))
;
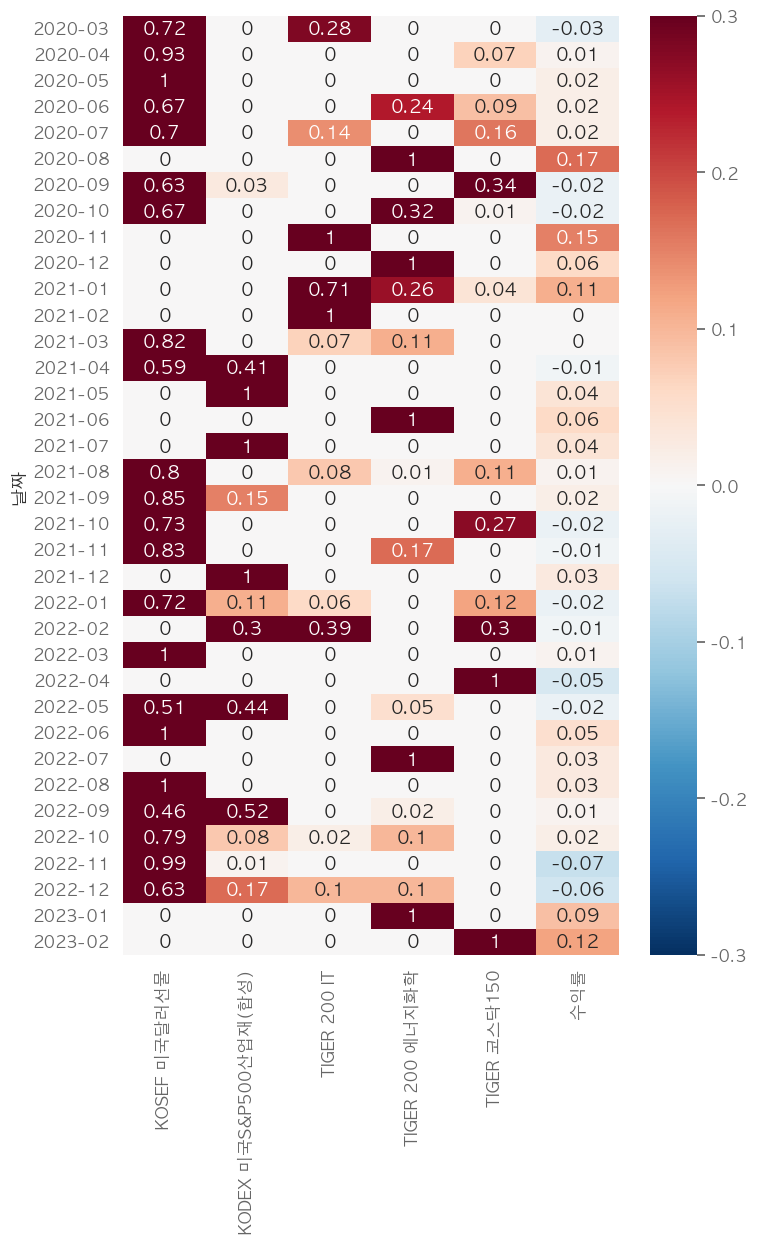
# 추천 투자 비중
msr_w_df.iloc[-1].round(2)
종목명
KOSEF 미국달러선물 0.22
KODEX 미국S&P500산업재(합성) 0.00
TIGER 200 IT 0.78
TIGER 200 에너지화학 0.00
TIGER 코스닥150 0.00
Name: 2023-02-28 00:00:00, dtype: float64
벤치마크 비교
benchmark = qs.utils.download_returns("SPY")
benchmark = benchmark.tz_convert(None)
# 슬리피지 0.001 : 리밸런싱 수수료 등을 포함한 손실
qs.reports.full((port_rets.sum(axis=1)-0.001).iloc[12:], benchmark=benchmark, periods_per_year=12, match_dates=True)
Performance Metrics
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2017-01-31 2017-01-31
End Period 2023-02-28 2023-02-28
Risk-Free Rate 0.0% 0.0%
Time in Market 100.0% 100.0%
Cumulative Return 254.64% 95.34%
CAGR﹪ 23.15% 11.64%
Sharpe 1.32 0.72
Prob. Sharpe Ratio 100.0% 95.07%
Smart Sharpe 1.21 0.66
Sortino 3.6 1.06
Smart Sortino 3.29 0.97
Sortino/√2 2.55 0.75
Smart Sortino/√2 2.33 0.69
Omega 3.2 3.2
Max Drawdown -12.89% -23.93%
Longest DD Days 304 393
Volatility (ann.) 16.62% 17.29%
R^2 0.13 0.13
Information Ratio 0.14 0.14
Calmar 1.8 0.49
Skew 1.14 -0.71
Kurtosis 1.58 1.19
Expected Daily % 1.73% 0.91%
Expected Monthly % 1.73% 0.91%
Expected Yearly % 19.82% 10.04%
Kelly Criterion 41.73% 27.28%
Risk of Ruin 0.0% 0.0%
Daily Value-at-Risk -6.06% -7.18%
Expected Shortfall (cVaR) -6.06% -7.18%
Max Consecutive Wins 8 13
Max Consecutive Losses 3 3
Gain/Pain Ratio 2.2 0.69
Gain/Pain (1M) 2.2 0.69
Payoff Ratio 1.52 0.69
Profit Factor 3.2 1.69
Common Sense Ratio 8.67 1.65
CPC Index 3.15 0.82
Tail Ratio 2.71 0.98
Outlier Win Ratio 3.18 3.63
Outlier Loss Ratio 3.67 1.73
MTD 11.83% -2.51%
3M 5.8% 3.07%
6M 12.05% -2.69%
YTD 21.46% 4.05%
1Y 11.57% -10.5%
3Y (ann.) 25.74% 10.7%
5Y (ann.) 20.59% 9.87%
10Y (ann.) 23.15% 11.64%
All-time (ann.) 23.15% 11.64%
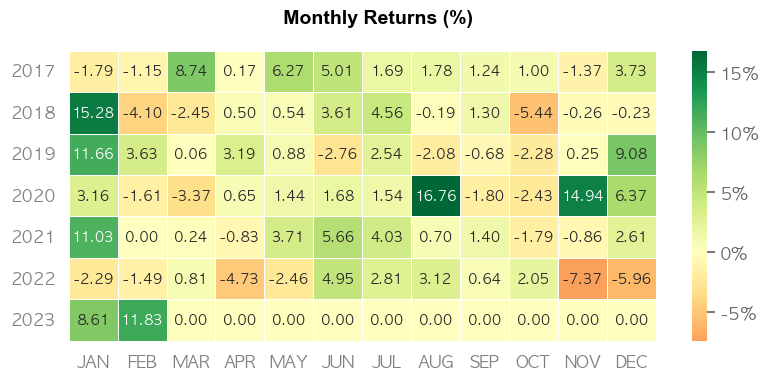
Best Day 16.76% 12.7%
Worst Day -7.37% -16.12%
Best Month 16.76% 12.7%
Worst Month -7.37% -16.12%
Best Year 41.4% 31.22%
Worst Year -10.24% -18.52%
Avg. Drawdown -4.82% -9.43%
Avg. Drawdown Days 105 121
Recovery Factor 19.75 3.98
Ulcer Index 0.03 0.08
Serenity Index 53.9 4.36
Avg. Up Month 4.18% 3.5%
Avg. Down Month -2.75% -5.06%
Win Days % 64.86% 70.27%
Win Month % 64.86% 70.27%
Win Quarter % 72.0% 76.0%
Win Year % 85.71% 71.43%
Beta 0.35 -
Alpha 0.18 -
Correlation 36.32% -
Treynor Ratio 729.41% -
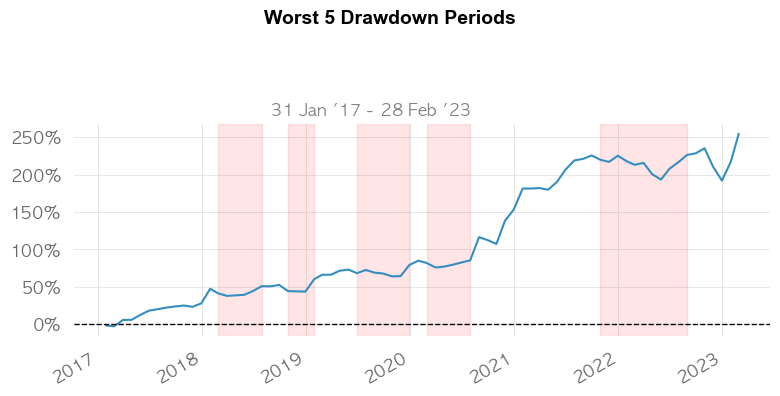
5 Worst Drawdowns
| Start | Valley | End | Days | Max Drawdown | 99% Max Drawdown | |
|---|---|---|---|---|---|---|
| 1 | 2022-11-30 | 2022-12-31 | 2023-02-28 | 90 | -12.893223 | -7.373604 |
| 2 | 2021-10-31 | 2022-05-31 | 2022-08-31 | 304 | -9.912068 | -7.639521 |
| 3 | 2018-02-28 | 2018-03-31 | 2018-07-31 | 153 | -6.449813 | -5.984983 |
| 4 | 2018-10-31 | 2018-12-31 | 2019-01-31 | 92 | -5.908822 | -5.692723 |
| 5 | 2019-06-30 | 2019-10-31 | 2019-12-31 | 184 | -5.238284 | -4.996693 |
Strategy Visualization
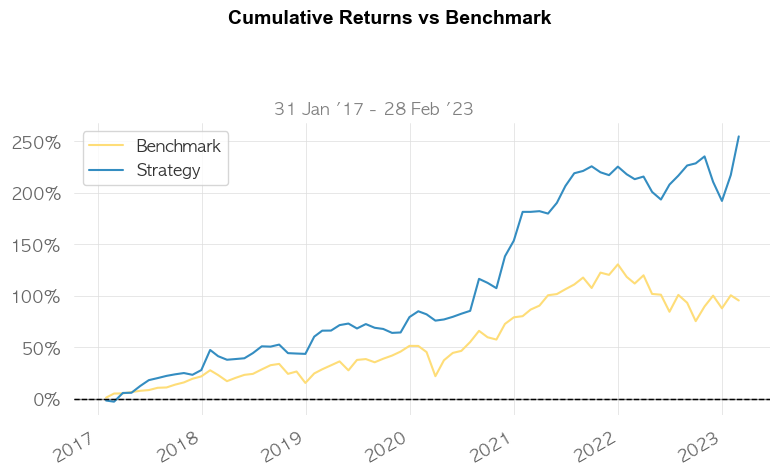
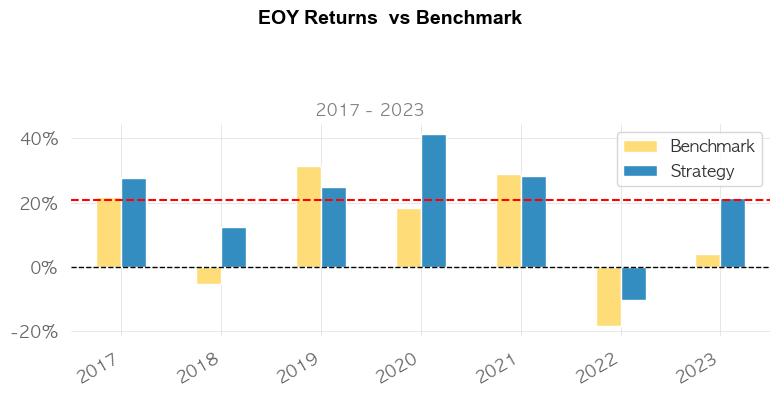
6. 결론
포트폴리오 최적화 결과, 최근 6년 수익률 254%와 샤프비율 1.32, MDD가 -13%가 나왔습니다.
포트폴리오 최적화 결과가 나왔다고 해서 반드시 해당 비중대로 투자를 해야 한다는 것은 아닙니다.
과거 수익률이 높다고 해서 미래에도 같은 수익률이 나올 것이라고 보장할 수는 없습니다.
또한, 투자자는 자신의 투자목표와 위험성향, 경제전망 등을 고려하여 투자 결정을 해야 합니다.
따라서, 해당 포트폴리오가 추천해주는 비중대로 투자를 하더라도, 투자자 스스로의 판단과 위험관리를 충분히 고려하여 투자를 결정하는 것이 바람직합니다.
S&P500을 능가하는 조합은 매우 드물지만, 조합을 찾아내었습니다.
그러나 장기적으로 한 종목만 선택한다면 S&P500이 가장 안정적인 선택일 것입니다.
5개의 종목을 랜덤하게 선택하여 결과를 분석해보았지만, 좋은 성과를 얻기 어려웠습니다.
따라서 유전 알고리즘을 도입하여 성능을 개선했습니다. 유전 알고리즘은 좋은 부모 유전자(종목)를 가질 경우 성능이 빨리 개선되는 것으로 나타났습니다.
그러나 좋은 부모 유전자(종목)를 가지고 있지 않으면 지역 최적해에서 벗어나지 못하여 포트폴리오 성능이 개선되지 않을 수 있습니다.
모든 데이터를 사용하여 최적의 종목을 찾기 위해 학습을 수행했습니다. 그러나 이러한 결과는 아직 검증되지 않았습니다.
최종적으로, 랜덤 및 유전 알고리즘으로 나온 좋은 결과를 바탕으로 포트폴리오를 구성했으며, 이를 기반으로 종목을 조금씩 교체하여 최고의 선택지를 찾아내었습니다.
일반적으로 포트폴리오라고 하기에는 보유하는 종목의 개수가 너무 적다보니 과거엔 수익률이 좋았지만 실제 투자시 위험에 노출될 확률이 높습니다.
계속해서 개선 방안을 찾아보고 있습니다. 좋은 아이디어 있으시다면 언제든지 제안해주시기 바랍니다. 감사합니다.
댓글남기기